Video: Kā atrisināt ierobežojumus ar kvadrātsaknēm?
2024 Autors: Miles Stephen | [email protected]. Pēdējoreiz modificēts: 2023-12-15 23:38
VIDEO
Kāda tad ir 1 bezgalības vērtība?
Būtībā, 1 dalīts ar ļoti lielu skaitli, kļūst ļoti tuvu nullei, tāpēc… 1 dalīts ar bezgalība , ja jūs patiešām varētu sasniegt bezgalība , ir vienāds ar 0.
Papildus iepriekš minētajam, kā jūs aprēķināt ierobežojumus? Atrodiet robežu, atrodot mazāko kopsaucēju
- Augšpusē atrodiet frakciju LCD.
- Sadaliet skaitītājus augšpusē.
- Pievienojiet vai atņemiet skaitītājus un pēc tam atceliet terminus.
- Izmantojiet daļskaitļu noteikumus, lai vienkāršotu to tālāk.
- Aizstājiet šo funkciju ar robežvērtību un vienkāršojiet.
Bez tam, kas ir kvadrātsakne no bezgalības?
Atbilde un skaidrojums: kvadrātsakne no bezgalības ir bezgalība . Ja jūs izvēlētos skaitli un reizinātu to ar sevi, jums tas būtu kvadrātā numurs.
Kā reizināt kvadrātsaknes?
Uz reiziniet kvadrātsaknes , pirmkārt vairoties radikādi vai skaitļi zem radikālas zīmes. Ja radikālas zīmes priekšā ir kādi koeficienti, vairoties tos arī kopā. Visbeidzot, ja jauno radikānu var sadalīt ar perfektu kvadrāts , ņemiet vērā šo ideālo kvadrāts un vienkāršot to.
Ieteicams:
Kā atrisināt kvadrātvienādojumu, izmantojot nulles koeficienta likumu?
No tā mēs varam secināt, ka: ja jebkuru divu skaitļu reizinājums ir nulle, tad viens vai abi skaitļi ir nulle. Tas ir, ja ab = 0, tad a = 0 vai b = 0 (kas ietver iespēju, ka a = b = 0). To sauc par nulles koeficienta likumu; un mēs to bieži izmantojam kvadrātvienādojumu risināšanai
Kā jūs atrisināt ideālās gāzes likumu?
Ideālās gāzes likuma formula Ideālās gāzes likuma formulas jautājumi: Atbilde: tilpums ir V = 890,0 ml un temperatūra ir T = 21°C un spiediens ir P = 750 mmHg. PV = nRT. Atbilde: Molu skaits ir n = 3,00 moli, temperatūra ir T = 24°C un spiediens P = 762,4 mmHg. PV = nRT
Kāpēc mēs nosakām ierobežojumus racionālai izpausmei un kad mēs nosakām ierobežojumus?
Mēs norādām ierobežojumus, jo dažās x vērtībās vienādojums var būt nedefinēts. Visizplatītākais ierobežojums racionālām izteiksmēm ir N/0. Tas nozīmē, ka jebkurš skaitlis, kas dalīts ar nulli, nav definēts. Piemēram, funkcijai f(x) = 6/x², aizstājot x=0, rezultāts būs 6/0, kas nav definēts
Kā lietot izmēru ierobežojumus programmā AutoCAD?
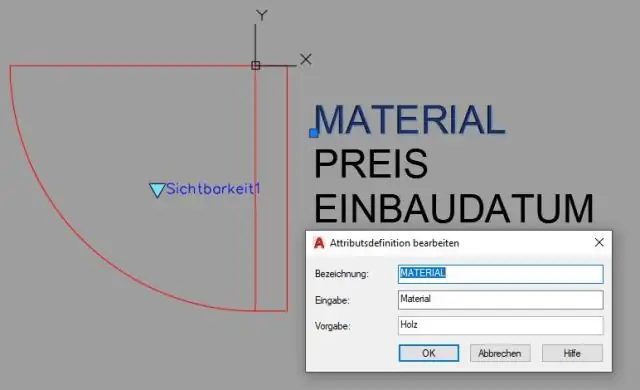
Šīs darbības parāda vienkāršu izmēru ierobežojumu piemēru: Sāciet jaunu zīmējumu un padariet lentes parametru cilni aktuālu. Statusa joslā ieslēdziet atbilstošos precīzās zīmēšanas palīglīdzekļus, piemēram, Snap, Ortho un Osnap. Uzzīmējiet pietiekami precīzu ģeometriju, izmantojot precīzas tehnikas
Kā jūs atrodat racionālas izteiksmes ierobežojumus?
Ierobežojums ir tāds, ka saucējs nevar būt vienāds ar nulli. Tātad šajā uzdevumā, jo 4x ir saucējā, tas nevar būt vienāds ar nulli. Atrodiet visas x vērtības, kuru saucējā ir nulle. Lai atrastu racionālas funkcijas ierobežojumus, atrodiet mainīgā vērtības, kas padara saucēju vienādu ar 0