Satura rādītājs:
- Kā: ņemot vērā funkciju, atspoguļojiet grafiku gan vertikāli, gan horizontāli
- Funkcijas tulkošanas/transformācijas noteikumi:
Video: Kā jūs atspoguļojat lineāro funkciju?
2024 Autors: Miles Stephen | [email protected]. Pēdējoreiz modificēts: 2023-12-15 23:38
A funkciju var būt atspoguļots ap asi, reizinot ar negatīvo. Uz atspoguļot ap y asi, reiziniet katru x ar -1, lai iegūtu -x. Uz atspoguļot ap x asi, reiziniet f(x) ar -1, lai iegūtu -f(x).
Kā šādā veidā atspoguļot funkciju?
Kā: ņemot vērā funkciju, atspoguļojiet grafiku gan vertikāli, gan horizontāli
- Reiziniet visas izejas ar –1, lai iegūtu vertikālu atspulgu. Jaunais grafiks ir sākotnējā grafika atspoguļojums ap x asi.
- Reiziniet visas ievades ar –1, lai iegūtu horizontālu atspulgu.
Turklāt, kas ir vienmērīga funkcija? Vienmērīga funkcija . A funkciju ar grafiku, kas ir simetrisks attiecībā pret y asi. A funkciju ir pat tad un tikai tad, ja f(–x) = f(x).
Turklāt, kā zināt, vai funkcija ir atspoguļota?
Tas ir, ja mēs atspoguļojam vienmērīgu funkciju y asī tas izskatīsies tieši tāpat kā oriģināls. Piezīme ja mēs atspoguļojam grafiku y asī, mēs iegūstam to pašu grafiku (vai mēs varētu teikt, ka tas "maps onto" pats). Savādi funkciju ir īpašība f(−x) = −f(x).
Kā pārveidot funkciju?
Funkcijas tulkošanas/transformācijas noteikumi:
- f (x) + b novirza funkcijas b vienības uz augšu.
- f (x) – b novirza funkcijas b vienības uz leju.
- f (x + b) pārvieto funkcijas b vienības pa kreisi.
- f (x – b) nobīda funkcijas b vienības pa labi.
- –f (x) atspoguļo funkciju x asī (tas ir, otrādi).
Ieteicams:
Kā lineāro nevienādību un lineāro vienādojumu risināšana ir līdzīga?
Lineāro nevienādību risināšana ir ļoti līdzīga lineāro vienādojumu risināšanai. Galvenā atšķirība ir tā, ka, dalot vai reizinot ar negatīvu skaitli, tiek apgriezta nevienlīdzības zīme. Lineāro nevienādību attēlošanai ir vēl dažas atšķirības. Ēnotā daļa ietver vērtības, kurās ir patiesa lineārā nevienādība
Kā jūs kvadrātā piešķirat funkciju?
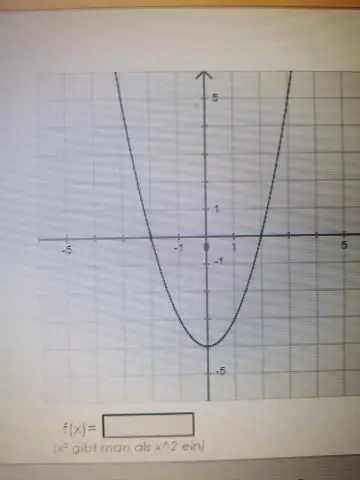
Kvadrātsaknes funkcija ir funkcija viens pret vienu, kas izmanto nenegatīvu skaitli kā ievadi un atgriež šī skaitļa kvadrātsakni kā izvadi. Piemēram, skaitlis 9 tiek kartēts ar skaitli 3. Kvadrātveida funkcija izmanto jebkuru skaitli (pozitīvu vai negatīvu) kā ievadi un atgriež šī skaitļa kvadrātu kā izvadi
Kā vertikāli samazināt lineāro funkciju?
Kā: ņemot vērā lineārās funkcijas vienādojumu, izmantojiet transformācijas, lai attēlotu lineāro funkciju formā f(x)=mx+b f (x) = m x + b. Grafiks f(x)=x f (x) = x. Vertikāli izstiepiet vai saspiediet grafiku par koeficientu |m
Kāds ir lineāro funkciju mērķis?
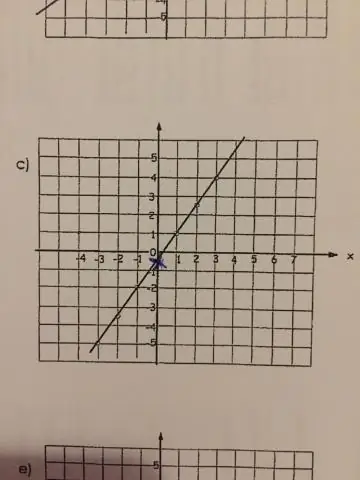
Lineāra funkcija ir jebkura funkcija, kas grafiski veido taisnu līniju. Matemātiski tas nozīmē, ka funkcijai ir viens vai divi mainīgie bez eksponentiem vai pakāpēm. Ja funkcijai ir vairāk mainīgo, mainīgajiem ir jābūt konstantēm vai zināmiem mainīgajiem, lai funkcija paliktu lineāra funkcija
Kādi ir daži lineāro funkciju piemēri dzīvē?
Sākotnējā atbilde: vai kāds varētu man sniegt piemēru par lineāro funkciju reālo situāciju? Lineārās funkcijas notiek jebkurā laikā, kad jums ir nemainīgs izmaiņu ātrums. Reālās dzīves piemēri ir šādi: 1., 2., 3. dienā patērētās strāvas atrašana… Jūs paņemat automašīnu nomai. Jūs braucat ar automašīnu ar ātrumu 60 km/h