Satura rādītājs:
Video: Kā krustproduktam izmantot labās rokas likumu?
2024 Autors: Miles Stephen | [email protected]. Pēdējoreiz modificēts: 2023-12-15 23:38
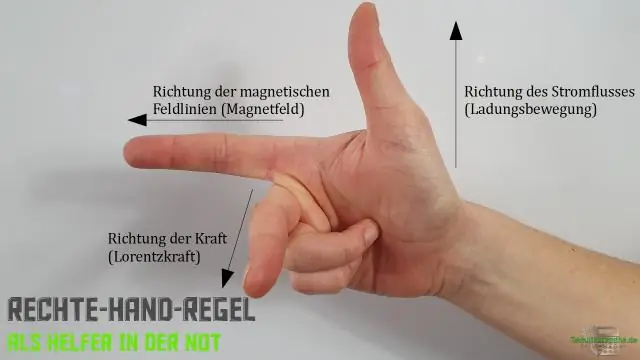
The taisnība - rokas likums norāda, ka vektoru orientācija krusta produkts tiek noteikts, novietojot un no asti līdz asti, saplacinot labā roka , pagarinot to virzienā un pēc tam saliekot pirkstus virzienā, ko leņķis veido ar. The īkšķis tad norāda virzienā uz.
Tātad, kā jūs veicat labās rokas likumu krusteniskajam produktam?
The krusta produkts vienmēr būs cits vektors, kas ir perpendikulārs abiem sākotnējiem vektoriem. Virziens krusta produkts tiek atrasts, izmantojot labās rokas noteikums , savukārt lielums krusta produkts To nosaka: Griezes moments ir spēka tendence izraisīt objekta griešanos.
kāds ir krustenisko produktu noteikums? The krusta produkts a × b ir definēts kā a vektors c, kas ir perpendikulārs (ortogonāls) gan pret a, gan b, ar labās puses virzienu noteikums un lielums, kas vienāds ar paralelograma laukumu, ko vektors aptver.
Var arī jautāt, kā jūs izmantojat labās rokas likumu?
Šķērsprodukta virzienu var atrast, piemērojot labās rokas likumu šādi:
- Rādītājpirksts norāda ātruma vektora v virzienā.
- Vidējais pirksts norāda magnētiskā lauka vektora B virzienā.
- Īkšķis ir vērsts krustprodukta F virzienā.
Kā aprēķināt šķērsproduktu?
Mēs varam aprēķināt uz Krusta produkts šādā veidā: Tātad garums ir: garums a reizināts ar garumu b reizināts ar leņķa starp a un b sinusu, tad mēs reizinām ar vektoru n, lai pārliecinātos, ka tas virzās pareizajā virzienā (taisnstūrī gan pret a, gan b).
Ieteicams:
Kā atrisināt kvadrātvienādojumu, izmantojot nulles koeficienta likumu?
No tā mēs varam secināt, ka: ja jebkuru divu skaitļu reizinājums ir nulle, tad viens vai abi skaitļi ir nulle. Tas ir, ja ab = 0, tad a = 0 vai b = 0 (kas ietver iespēju, ka a = b = 0). To sauc par nulles koeficienta likumu; un mēs to bieži izmantojam kvadrātvienādojumu risināšanai
Kā jūs atrisināt ideālās gāzes likumu?
Ideālās gāzes likuma formula Ideālās gāzes likuma formulas jautājumi: Atbilde: tilpums ir V = 890,0 ml un temperatūra ir T = 21°C un spiediens ir P = 750 mmHg. PV = nRT. Atbilde: Molu skaits ir n = 3,00 moli, temperatūra ir T = 24°C un spiediens P = 762,4 mmHg. PV = nRT
Kādas ir labas kartes pamatīpašības?
Dažas kopīgas karšu funkcijas ir mērogs, simboli un režģi. Visas kartes ir realitātes mēroga modeļi. Amap mērogs norāda saistību starp attālumu kartē un faktiskajiem attālumiem uz Zemes
Kāda ir P rokas funkcija?
“P” nāk no franču valodas “petit”, kas nozīmē mazs. Visām cilvēka hromosomām ir 2 rokas - p (īsā) un q (garā) -, kuras viena no otras atdala tikai primārais sašaurinājums, centromērs, punkts, kurā hromosoma ir pievienota vārpstai šūnu dalīšanās laikā
Kāda ir atšķirība starp sabiedrības likumu un zinātnisko likumu?
Sabiedrības likumi. Zinātniskie likumi ir balstīti uz zinātniskiem pierādījumiem, ko atbalsta eksperimenti. Zinātnisko likumu piemēri. Sabiedrības likumi ir balstīti uz sabiedrības valdības uzvedību un rīcību