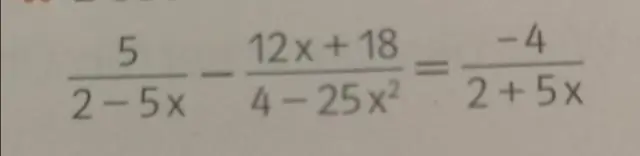
Satura rādītājs:
Video: Kā atrisināt lineārās programmēšanas problēmu ar stūru metodi?
2024 Autors: Miles Stephen | [email protected]. Pēdējoreiz modificēts: 2023-12-15 23:38
THE STŪRU METODE Iezīmējiet iespējamo kopu (reģionu), S. Atrodi precīzas visu virsotņu koordinātas ( stūrī punkti) no S. Novērtējiet mērķa funkciju P katrā virsotnē Maksimums (ja tāds pastāv) ir P lielākā vērtība virsotnē. Minimums ir mazākā P vērtība virsotnē.
Pēc tam var arī jautāt, kādas ir metodes LPP risināšanai?
Lineārās programmēšanas uzdevumu risināšanas grafiskā metode
- Ieteiktie video.
- 1. darbība. Formulējiet LP (lineārās programmēšanas) problēmu.
- 2. darbība: izveidojiet grafiku un uzzīmējiet ierobežojumu līnijas.
- 3. darbība: nosakiet katras ierobežojuma līnijas derīgo pusi.
- 4. darbība: nosakiet iespējamo risinājuma reģionu.
- 5. darbība. Uzzīmējiet mērķa funkciju grafikā.
- 6. darbība: atrodiet optimālo punktu.
kas ir algebriskā metode lineārajā programmēšanā? Algebra un Simplex Metode . A Lineārās programmēšanas problēma (LP) ir an optimizācijas problēma ja visi mainīgie ir nepārtraukti, mērķis ir a lineārs (attiecībā uz lēmuma mainīgajiem) funkcija, un iespējamais apgabals ir noteikts ar ierobežotu skaitu lineārs nevienādības vai vienādojumi.
Kā aprēķināt stūra punktus lineārajā programmēšanā?
The stūra punkti ir iespējamā reģiona virsotnes. Kad jums ir sistēmas grafiks lineārs nevienādības, tad varat apskatīt grafiku un viegli noteikt, kur stūra punkti ir. Jums var būt nepieciešams atrisināt sistēmu lineārs vienādojumi ar atrast dažas no koordinātām punktus vidū.
Kāda ir stūra punkta risināšanas metode?
The stūra punkta risinājuma metode sastāv no četriem galvenajiem soļiem:: Nosakiet katras virsotnes koordinātas ( stūra punkts ) no iespējamā reģiona.: aprēķina mērķa funkcijas vērtību katrā stūra punkts .: iestatiet mērķa funkciju ar maksimālo vērtību.
Ieteicams:
Kā atrisināt proporciju problēmu?
Vispirms uzrakstiet proporciju, izmantojot burtu, lai apzīmētu trūkstošo terminu. Mēs atrodam krustojumu, reizinot 20 reizes x un 50 reizes 30. Pēc tam daliet, lai atrastu x. Rūpīgi izpētiet šo soli, jo šī ir metode, kuru mēs bieži izmantosim algebrā
Kā atrisināt slīpuma problēmu?
Identificējiet slīpumu, m. To var izdarīt, aprēķinot slīpumu starp diviem zināmiem līnijas punktiem, izmantojot slīpuma formulu. Atrodiet y krustpunktu. To var izdarīt, slīpuma pārtveršanas formulā aizvietojot slīpumu un punkta (x, y) koordinātas uz līnijas un pēc tam atrisinot b
Kādi ir lineārās programmēšanas pieņēmumi?
Lineārās programmēšanas noteiktības nosacījumu pieņēmumi. Tas nozīmē, ka skaitļi mērķī un ierobežojumi ir noteikti zināmi un mainās pētāmā laika posmā. Linearitāte vai proporcionalitāte. Aditīvi. Dalāmība. Nenegatīvs mainīgais. Galīgums. Optimalitāte
Kas ir lineārās programmēšanas simpleksā metode?
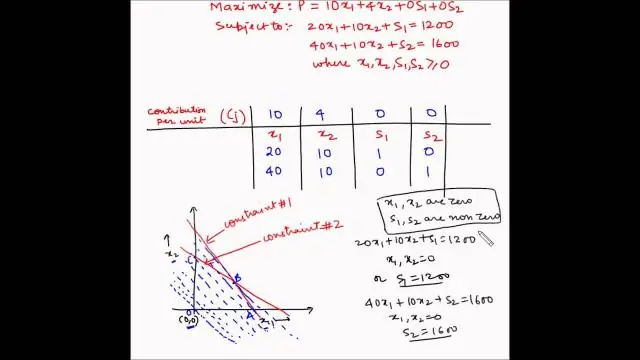
Vienkāršā metode. Simpleksā metode, Standarta tehnika lineārās programmēšanas optimizācijas problēmas risināšanai, parasti tāda, kas ietver funkciju un vairākus ierobežojumus, kas izteikti kā nevienlīdzības. Nevienādības nosaka daudzstūra apgabalu (sk. daudzstūri), un risinājums parasti atrodas vienā no virsotnēm
Kā atrisināt lineārās izteiksmes?
Lai atrisinātu lineāros vienādojumus, mēs plaši izmantosim šādus faktus. Ja a=b, tad a+c=b+c a + c = b + c jebkuram c. Lineāro vienādojumu risināšanas process Ja vienādojumā ir daļskaitļi, izmantojiet mazāko kopsaucēju, lai notīrītu daļskaitļus. Vienkāršojiet abas vienādojuma puses