Video: Kāpēc mēs nosakām ierobežojumus racionālai izpausmei un kad mēs nosakām ierobežojumus?
2024 Autors: Miles Stephen | [email protected]. Pēdējoreiz modificēts: 2023-12-15 23:38
Mēs norādām ierobežojumus jo dažās x vērtībās vienādojums var būt nedefinēts. Visbiežāk racionālu izteicienu ierobežojums ir N/0. Tas nozīmē, ka jebkurš skaitlis, kas dalīts ar nulli, nav definēts. Piemēram, funkcijai f(x) = 6/x², aizstājot x=0, tā būtu rezultāts uz 6/0, kas nav definēts.
Tāpat jūs varat jautāt, vai racionālai izteiksmei nevar būt nekādu ierobežojumu?
Nu tas pats ir patiess priekš racionālas izpausmes . Otrais racionāla izteiksme ir nekad nav nulle saucējā, un tāpēc mēs to nedarām nepieciešams par ko uztraukties jebkuri ierobežojumi . Ņemiet vērā arī to, ka otrā skaitītājs racionāla izpausme griba būt nulle. Tas ir labi, mēs vienkārši nepieciešams lai izvairītos no dalīšanas ar nulli.
Kā arī risinat racionālas izteiksmes? Racionāla vienādojuma atrisināšanas soļi ir šādi:
- Atrodiet kopsaucēju.
- Reiziniet visu ar kopsaucēju.
- Vienkāršot.
- Pārbaudiet atbildi(-es), lai pārliecinātos, ka nav sveša risinājuma.
Līdzīgi var jautāt, kā jūs atrodat racionālas funkcijas ierobežojumus?
The ierobežojums ir tas, ka saucējs nevar būt vienāds ar nulli. Tātad šajā uzdevumā, jo 4x ir saucējā, tas nevar būt vienāds ar nulli. Atrast visas x vērtības, kas saucējā dod nulli. Uz atrast ierobežojumus uz racionāla funkcija , atrast mainīgā lieluma vērtības, kas padara saucēju vienādu ar 0.
Kādi ir mainīgie ierobežojumi?
The ierobežojumiem ir saucējā, nevis skaitītājā 2. Nav iespējams, ka saucējā ir termins, kas satur mainīgs vienāds ar nulli. Ja tā notiek, tas kļūst par a ierobežojums.
Ieteicams:
Kāpēc ampērmetrā ir rādījums, kad ķēde ir aizvērta?
Atverot un aizverot ampērmetru, apļveida magnētiskais materiāls uzņems induktivitāti, kas tos pastiprina līdz spriegumam, kas virza skaitītāju. Jo lielāka strāva, jo lielāks spriegums. Tādējādi jūs varat iegūt diezgan precīzu strāvas nolasījumu, kas plūst slēgtā ķēdē
Kā lietot izmēru ierobežojumus programmā AutoCAD?
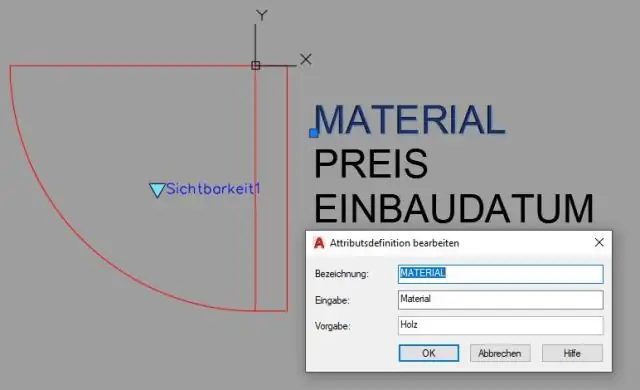
Šīs darbības parāda vienkāršu izmēru ierobežojumu piemēru: Sāciet jaunu zīmējumu un padariet lentes parametru cilni aktuālu. Statusa joslā ieslēdziet atbilstošos precīzās zīmēšanas palīglīdzekļus, piemēram, Snap, Ortho un Osnap. Uzzīmējiet pietiekami precīzu ģeometriju, izmantojot precīzas tehnikas
Kā jūs atrodat racionālas izteiksmes ierobežojumus?
Ierobežojums ir tāds, ka saucējs nevar būt vienāds ar nulli. Tātad šajā uzdevumā, jo 4x ir saucējā, tas nevar būt vienāds ar nulli. Atrodiet visas x vērtības, kuru saucējā ir nulle. Lai atrastu racionālas funkcijas ierobežojumus, atrodiet mainīgā vērtības, kas padara saucēju vienādu ar 0
Kā atrisināt ierobežojumus ar kvadrātsaknēm?
VIDEO Kāda tad ir 1 bezgalības vērtība? Būtībā, 1 dalīts ar ļoti lielu skaitli, kļūst ļoti tuvu nullei, tāpēc… 1 dalīts ar bezgalība , ja jūs patiešām varētu sasniegt bezgalība , ir vienāds ar 0. Papildus iepriekš minētajam, kā jūs aprēķināt ierobežojumus?
Kad jāizmanto korelācija un kad jāizmanto vienkārša lineārā regresija?
Regresiju galvenokārt izmanto, lai izveidotu modeļus/vienādojumus, lai prognozētu galveno reakciju Y no prognozējošo (X) mainīgo kopas. Korelāciju galvenokārt izmanto, lai ātri un kodolīgi apkopotu attiecību virzienu un stiprumu starp 2 vai vairāku skaitlisku mainīgo kopu