Satura rādītājs:
Video: Kā jūs pārveidojat lineārās funkcijas?
2024 Autors: Miles Stephen | [email protected]. Pēdējoreiz modificēts: 2023-12-15 23:38
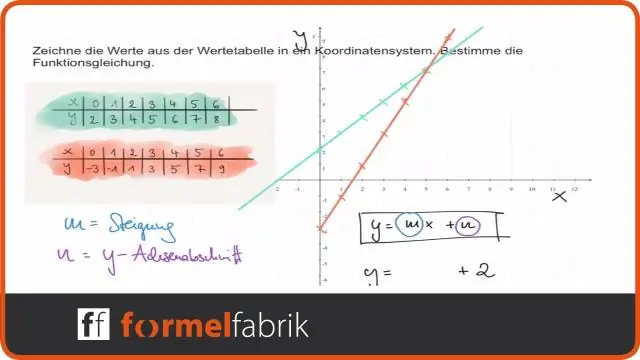
Kā: ņemot vērā a vienādojumu lineārā funkcija , izmantojiet pārvērtības lai attēlotu grafiku lineārā funkcija formā f(x)=mx+b f (x) = m x + b. Grafiks f(x)=x f (x) = x. Vertikāli izstiepiet vai saspiediet grafiku par koeficientu |m|. Pārbīdiet diagrammu uz augšu vai uz leju b vienības.
Tātad, kā jūs raksturojat lineāras funkcijas transformāciju?
Grafiks a lineārā funkcija (līnija) var pārvietot ap koordinātu režģi. To sauc par a transformācija . Ir trīs pamata pārvērtības : tulkošana (līnijas bīdīšana apkārt), atspulgs (līnijas pagriešana) un mērogošana (līnijas izstiepšana). Jūs varat pārvietoties ( pārveidot ) līniju vertikāli vai horizontāli.
Kā arī, kuras transformācijas ietekmē lineārās funkcijas slīpumu? Pārveidojoties Lineārās funkcijas (Stiepšana un saspiešana) Izstiepumi un kompresijas maina lineāras funkcijas slīpums . Ja līnija kļūst stāvāka, funkciju ir izstiepts vertikāli vai saspiests horizontāli.
Attiecīgi, kā pārveidot funkciju?
Funkcijas tulkošanas/transformācijas noteikumi:
- f (x) + b novirza funkcijas b vienības uz augšu.
- f (x) – b novirza funkcijas b vienības uz leju.
- f (x + b) pārvieto funkcijas b vienības pa kreisi.
- f (x – b) nobīda funkcijas b vienības pa labi.
- –f (x) atspoguļo funkciju x asī (tas ir, otrādi).
Kā jūs atspoguļojat funkciju?
A funkciju var būt atspoguļots ap asi, reizinot ar negatīvo. Uz atspoguļot ap y asi, reiziniet katru x ar -1, lai iegūtu -x. Uz atspoguļot ap x-asi reiziniet f(x) ar -1, lai iegūtu -f(x).
Ieteicams:
Kā jūs EBD pārveidojat par angstrēmiem?
Konstantes un konversijas koeficienti 1 Angstrom (A) atbilst 12398 eV (vai 12,398 keV), un attiecība ir apgriezta saskaņā ar Ephoton = hν = hc/λ. Tātad E(eV) = 12398/λ(A) vai λ(A) = 12398/E(eV) = 12,398/E(keV). Ņemiet vērā, ka varat apvienot iepriekš minēto ar faktiem, lai saistītu viļņu garumus ar temperatūru
Kā jūs vērtējat saliktās funkcijas?
Salikto funkciju novērtēšana, izmantojot grafikus Atrodiet doto ievadi iekšējai funkcijai uz tās grafika x-ass. Nolasiet iekšējās funkcijas izvadi no tās grafika y ass. Atrodiet iekšējās funkcijas izvadi uz ārējās funkcijas grafika x-ass
Kā jūs veidojat vecāku funkcijas grafiku?
Funkcija y=x2 vai f(x) = x2 ir kvadrātfunkcija, un tā ir visu pārējo kvadrātfunkciju vecāku grafiks. Funkcijas f(x) = x2 diagrammas saīsne ir jāsāk ar punktu (0, 0) (izcelsme) un jāatzīmē punkts, ko sauc par virsotni. Ņemiet vērā, ka punkts (0, 0) ir tikai vecākfunkcijas virsotne
Kā jūs vienkāršojat lineārās izteiksmes?
VIDEO Tad kā vienkāršot izteiksmi? Tālāk ir norādītas pamata darbības, kas jāveic, lai vienkāršotu algebrisko izteiksmi noņemiet iekavas, reizinot koeficientus. izmantojiet eksponentu noteikumus, lai noņemtu iekavas attiecībā uz eksponentiem.
Kā jūs salīdzināt lineārās attiecības?
VIDEO Turklāt kādi ir daži lineāro attiecību piemēri? Lineāras attiecības piemēram, y = 2 un y = x visas diagrammas tiek attēlotas kā taisnas līnijas. Grafikējot y = 2, jūs iegūstat līniju, kas iet horizontāli pie uz 2 atzīme uz uz y ass.