
Satura rādītājs:
- Autors Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:38.
- Pēdējoreiz modificēts 2025-01-22 17:05.
Logaritmisko funkciju grafēšana
- The grafikā no apgrieztās funkciju no jebkura funkciju ir atspoguļojums grafikā no funkciju par līniju y=x.
- The logaritmiskā funkcija , y= žurnāls b(x), var pārvietot k vienības vertikāli un h vienības horizontāli ar vienādojumu y= žurnāls b(x+h)+k.
- Apsveriet logaritmiskā funkcija y=[ žurnāls 2(x+1)−3].
Ņemot to vērā, kā attēlot negatīvos žurnālus?
Pirmais ir tad, kad mums ir a negatīvs zīme. Kad tas notiks, mūsu grafikā apvērsīsies vai nu pār y asi, vai pār x asi. Ass, kas grafikā apgāžas ir atkarīgs no tā, kur negatīvs zīme ir. Kad negatīvs zīme ir argumentā par žurnāla funkcija , grafikā apgriežas pāri y asij.
Tāpat, kas ir logaritmiskās funkcijas piemērs? Logaritms , eksponents vai pakāpe, līdz kurai jāpalielina bāze, lai iegūtu noteiktu skaitli. Izsakot matemātiski, x ir logaritms no n uz bāzi b, ja bx = n, tādā gadījumā raksta x = logb n. Priekš piemērs , 23 = 8; tāpēc 3 ir logaritms no 8 līdz 2. bāzei vai 3 = žurnāls2 8.
Līdzīgi, kas ir logaritmiskās funkcijas?
Logaritmiskās funkcijas ir eksponenciālas apgrieztās vērtības funkcijas . Eksponenciālā apgrieztā vērtība funkciju y = ax ir x = ay. The logaritmiskā funkcija y = žurnālsax ir definēts kā ekvivalents eksponenciālajam vienādojumam x = ay. y = žurnālsax tikai šādos apstākļos: x = ay, a > 0 un a≠1.
Kāpēc mēs izmantojam logaritmiskos grafikus?
Tur ir divi galvenie iemesli izmantot logaritmu skalas diagrammās un grafiki . Pirmais ir reaģēt uz šķībību pret lielām vērtībām; i., gadījumi, kuros viens vai daži punkti ir daudz lielāks nekā lielākā daļa datu. Otrais ir lai parādītu procentuālās izmaiņas vai reizināšanas faktorus.
Ieteicams:
Kā jūs attēlojat ātrumu un paātrinājumu?

Princips ir tāds, ka līnijas slīpums ātruma un laika grafikā atklāj noderīgu informāciju par objekta paātrinājumu. Ja paātrinājums ir nulle, tad slīpums ir nulle (t.i., horizontāla līnija). Ja paātrinājums ir pozitīvs, tad slīpums ir pozitīvs (t.i., uz augšu slīpa līnija)
Kā jūs vērtējat saliktās funkcijas?
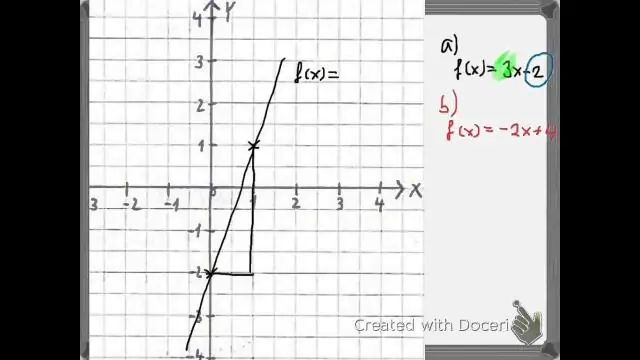
Salikto funkciju novērtēšana, izmantojot grafikus Atrodiet doto ievadi iekšējai funkcijai uz tās grafika x-ass. Nolasiet iekšējās funkcijas izvadi no tās grafika y ass. Atrodiet iekšējās funkcijas izvadi uz ārējās funkcijas grafika x-ass
Kā kalkulatorā attēlot logaritmiskās funkcijas?

Grafiku kalkulatorā e bāzes logaritms ir atslēga ln. Visi trīs ir vienādi. Ja jums ir funkcija logBASE, to var izmantot, lai ievadītu funkciju (skatīt Y1 zemāk). Ja nē, izmantojiet bāzes maiņas formulu (skatiet Y2 zemāk)
Kas ir eksponenciālās un logaritmiskās funkcijas?
Logaritmiskās funkcijas ir eksponenciālo funkciju apgrieztās vērtības. Eksponenciālās funkcijas y = ax apgrieztā vērtība ir x = ay. Logaritmiskā funkcija y = logax ir definēta kā ekvivalenta eksponenciālajam vienādojumam x = ay. y = logax tikai šādos apstākļos: x = ay, a > 0 un a≠1
Kā jūs attēlojat racionālas izteiksmes?

Racionālas funkcijas diagrammas veidošanas process Atrodiet pārtvērumus, ja tādi ir. Atrodiet vertikālās asimptotes, iestatot saucēju vienādu ar nulli un atrisinot. Atrodiet horizontālo asimptotu, ja tāda pastāv, izmantojot iepriekš minēto faktu. Vertikālās asimptotes sadalīs skaitļu līniju reģionos. Skicējiet grafiku
